统计绘图函数

本章介绍通用的统计绘图函数，比如直方图、箱型图等。

[1]:

import numpy as np
from matplotlib import pyplot as plt

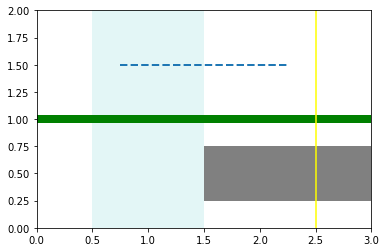
水平或竖直的线/矩形：ax.axhline / axhspan

用 axhline/axvline 绘制水平线/竖直线，用 axhspan/axvspan 绘制水平矩形/竖直矩形。

需要注意，下例中所有 xmin/xmax 参数是一个相对比例。比如 axhline 中的 xmin=0.25, xmax=0.75 表示从图像的左 1/4 处画起、到右 1/4 处结束。由于用 axis(...) 命令给出了横坐标的绘图范围是 [0, 3]，因此这个 axhline 实际上是从横坐标 0.75 处画到 2.25 处。

[2]:

f, ax = plt.subplots()

ax.axis([0, 3, 0, 2])
ax.axhline(1, lw=8, color='g')
ax.axhline(y=1.5, ls="--", lw=2, xmin=0.25, xmax=0.75)
ax.axvline(2.5, color="yellow")

ax.axhspan(0.25, 0.75, xmin=0.5, facecolor='0.5')
ax.axvspan(0.5, 1.5, facecolor="#74D2D5", alpha=0.2)

plt.show()

散点图：ax.scatter

散点图将多维（一般二维）数据用点绘制出来，一般是为了揭示不同维之间的关系。

如果不显示点的大小，最简单的散点图可以用 plot(..., '.') 绘制：

[3]:

np.random.seed(230)
x, y = np.random.rand(2, 10)

f, ax = plt.subplots()
ax.plot(x, y, '.')

plt.show()

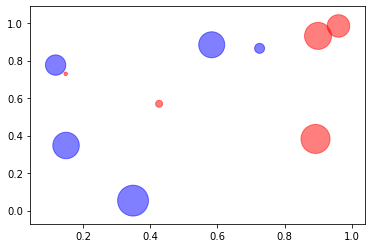
言归正传，正常的散点图用 ax.scatter(x, y, s=None, c=None, ...)：

s：数组，每个点的大小。
c：列表，每个点的颜色。
marker='o'：所有点的点样式。

[4]:

np.random.seed(233)
x, y = np.random.rand(2, 10)
np.random.seed(666)
point_size = 1000 * np.random.rand(10)

f, ax = plt.subplots()
ax.scatter(x, y, s=point_size, c=["b", "r"] * 5, alpha=0.5)
plt.show()

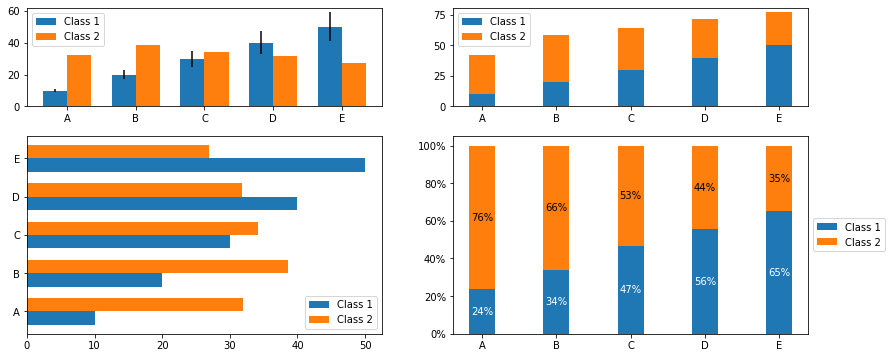
条形图：ax.bar / barh

条形图按多个分组来展示数据。用 bar 绘制竖立的条形图，或者用 barh 绘制横置的。

基本用法：

ax.bar(x, height, width=0.8, ...)

x：一维数组，长度与组个数相同，给出条形图的每组的水平位置。在默认的 align='center' 参数下，条形图每组的下端正中与 x 数组中每个元素对齐。你可以指定 align='edge' 来让每组的下端左侧与 x 中的位置对齐。
height：条形图的高，即数据。应该与 x 等长。
width：条形图的宽度。

下例的第四幅子图用到了 matplotlib.ticker.PercentFormatter 来将纵轴的刻度改为百分数，读者可以参考之前的坐标轴刻度章节，或者官方 Tick formatters 示例。

[5]:

import matplotlib.ticker as ticker

bar_width = 0.35
groups = np.arange(5)
y1 = np.linspace(10, 50, 5)
np.random.seed(0)
y2 = np.random.rand(5) * 40 + 10

f, ax = plt.subplots(2, 2, figsize=(14, 6), gridspec_kw = {'height_ratios':[1, 2]})
# 并列竖立条形图
ax[0,0].bar(groups, y1, bar_width, label="Class 1",
          yerr=2 * groups + 1)
ax[0,0].bar(groups + bar_width, y2, bar_width, label="Class 2")
ax[0,0].set_xticks(groups + bar_width / 2)
ax[0,0].set_xticklabels(list("ABCDE"))
ax[0,0].legend(loc="upper left")

# 堆叠竖立条形图
ax[0,1].bar(groups, y1, bar_width, label="Class 1")
ax[0,1].bar(groups, y2, bar_width, bottom=y1, label="Class 2")
ax[0,1].set_xticks(groups)
ax[0,1].set_xticklabels(list("ABCDE"))
ax[0,1].legend(loc="upper left")

# 横置条形图
ax[1,0].barh(groups, y1, bar_width, label="Class 1")
ax[1,0].barh(groups + bar_width, y2, bar_width, label="Class 2")
ax[1,0].set_yticks(groups + bar_width / 2)
ax[1,0].set_yticklabels(list("ABCDE"))
ax[1,0].legend(loc="lower right")

# 堆叠竖立百分比条形图（附百分比数字）
y1_percent = y1 / (y1 + y2)
y2_percent = y2 / (y1 + y2)
ax[1,1].bar(groups, y1_percent, bar_width, label="Class 1")
ax[1,1].bar(groups, y2_percent, bar_width, bottom=y1_percent, label="Class 2")
## 加上百分比字串
for k in range(len(groups)):
    ax[1,1].text(groups[k], y1_percent[k]/2, r"{:.0%}".format(y1_percent[k]),
                 color="w", ha="center", va="center")
    ax[1,1].text(groups[k], y2_percent[k]/2 + y1_percent[k],
                 r"{:.0%}".format(y2_percent[k]), color="k", ha="center", va="center")
ax[1,1].set_xticks(groups)
ax[1,1].set_xticklabels(list("ABCDE"))
ax[1,1].legend(loc="center left", bbox_to_anchor=(1.0, 0.5))
## 设置 y 轴刻度
ax[1,1].yaxis.set_major_formatter(ticker.PercentFormatter(xmax=1, decimals=0))

plt.show()

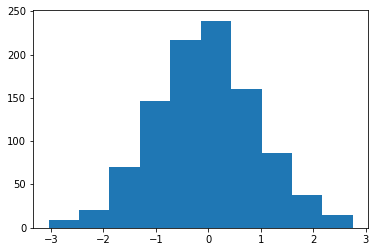
直方图：ax.hist

不同于条形图，直方图绘制的是一维的数据，展现数据的频数或者频率。

最简单的直方图 ax.hist(x)，可以是单参数的：

[6]:

np.random.seed(0)
x = np.random.normal(0, 1, 1000)  # 标准正态

f, ax = plt.subplots()
ax.hist(x)
plt.show()

下面是我认为的几个常用参数：

ax.hist(x, bins=None, density=None, weights=None, histtype='bar', ...)

x：直方图的一维数据。
bins：控制分组的参数。
- 如果传入整数，就会对应自动分为几组。
- 如果传入列表，会按列表中的数给出分组。比如 [1,2,3,4]，会将区间 [1,2) （左闭右开，即包含1不包含2）与 [2,3) 分为一组。但是列表中的最后一组将是双侧闭区间：[3,4]。
- 如果传入字符串（较少用到），请参考 Numpy 文档中 histogram_bin_edges¶ 函数的 bins 参数。
density：（不常使用）控制图像密度的参数。设为 True 时将在绘图时对数据进行归一化，使直方图下方的面积求和为 1。
- 该“面积求和为 1”与每个组的宽度有关，并不是常规统计意义上的密度。除非组宽是1，否则设置 density=True 并不能得到频率图；频率直方图可以参考 weights 参数。
- 旧版本有一个与现有的 density 参数相关的 normed 参数，但它即将被废弃。
weights：控制每个数据点的权重。常规的直方图每个数据点出现 1 次，就记 1 频数；因此每个数据点权重均是 1。下例的图 2 用数据点总数的倒数作为权重，给出了一个频率直方图的实现。
histtype：控制直方图类型。
- 'bar'：默认的直方图。多维数据会在组内并排排列。
- 'barstacked'：多维数据会在组内堆叠排列。。
- 'step'：用阶梯折线图（lineplot）代替了直方图，参考下例的图3。
- 'stepfilled'：下方用颜色填充的阶梯折线图。

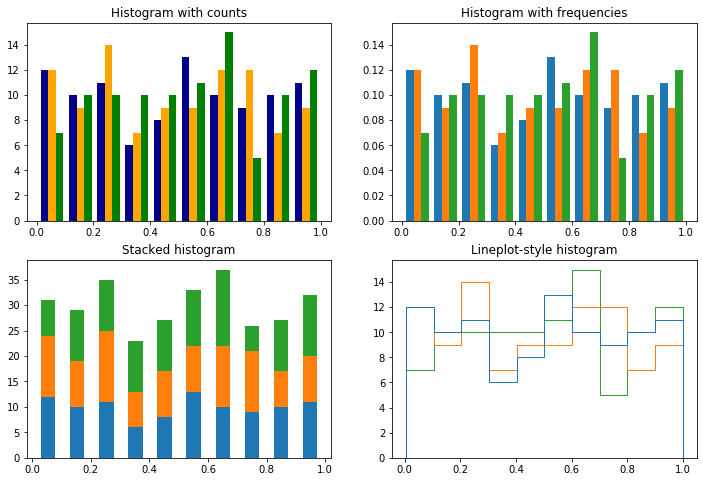
几个例子（注意例中各图纵坐标刻度的区别）：

[7]:

np.random.seed(0)
x = np.random.rand(100, 3)
bins_num = 10

f, ax = plt.subplots(2, 2, figsize=(12, 8))
ax = ax.ravel()

# 频数
ax[0].hist(x, bins_num, color=("darkblue", "orange", "g"))
ax[0].set_title("Histogram with counts")

# 频率
ax[1].hist(x, bins_num, weights=np.ones_like(x)/x.shape[0])
ax[1].set_title("Histogram with frequencies")

ax[2].hist(x, bins_num, histtype="bar", stacked=True, rwidth=0.5)
ax[2].set_title("Stacked histogram")

ax[3].hist(x, bins_num, histtype='step')
ax[3].set_title("Lineplot-style histogram")

plt.show()

核密度曲线

Matplotlib 没有简洁的核密度曲线图（kernel density plot）的实现，这件事恐怕自从 matplotlib 风靡之日起就在被吐槽。相比之下，基于 matplotlib 的 seaborn 库提供了一个很简单的 distplot 来实现这一功能，但在 matplotlib 里我们恐怕需要稍微多花一点功夫。

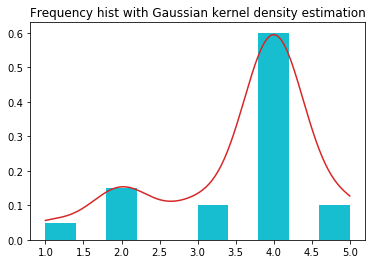
下例是频率直方图（通过 weights 参数转换为频率）与对应的 Gaussian 核密度曲线：

[8]:

from scipy.stats import gaussian_kde

values = list(range(1, 6))
freqs = [5, 15, 10, 60, 10]
x = np.concatenate([np.ones(f)*v for v, f in zip(values, freqs)])

density = gaussian_kde(x)
x_plot = np.linspace(min(x), max(x), 200)

f, ax = plt.subplots()
ax.hist(x, weights=np.ones_like(x)/len(x), color='tab:cyan')
ax.plot(x_plot, density(x_plot), 'tab:red')
ax.set_title("Frequency hist with Gaussian kernel density estimation")

plt.show()

gaussian_kde 函数的 bw_method 参数的默认值是 'scott' 方法，读者也可以选用 'silverman' 方法。除了接受这两种字串，bw_method 还可以直接接受数值作为 Scott factor（如上例）。默认的 Scott factor 的选值是：\(n^{-1/(d+4)}\)，其中 \(n\) 是数据长，\(d\) 是数据集的维度。

更多关于 bw_method 参数的细节可以参考 Scipy.stats.gaussian_kde 页面的内容。

饼图：ax.pie

我讨厌饼图！非常讨厌！如果你一定要画饼图，并且玩很多视觉花招，那我不建议你用 matplotlib 来实现。

饼图的绘制指令的常用参数：

ax.pie(x, explode=None, ...)

explode=None：控制扇形区域向外“炸开”的距离，传入一个数组。
radius=1：饼图半径。
labels=None, colors=None：扇形区的标签与颜色。
- labeldistance：标签到圆心的距离。
- rotatelabels=False：旋转标签，使其文字方向指向圆心。
autopct=None：显示百分数。可以传入一个格式化字串，或者一个函数。
- 如果原数据集已经是百分数，那么可以使用格式化字串 autopct="%.1f%%" 显示含一位小数的百分数。下例中使用了较复杂的函数实现来针对不同的数据集情况。
- pctdistance=0.6: 在 autopct 有效时使用，指定百分数标签到圆心的距离。
startangle=0：开始绘制饼图的角度，从 X 轴正向开始逆时针旋转。
counterclock=True：是否沿逆时针绘制，设为 False 是沿顺时针绘制。
其他绘图参数：
- wedgeprops：绘图属性，比如线型等。
- textprops：标签文字的属性。

[9]:

x = [[30], [20, 15], [45, 35, 25]]
x_flatten = [v for item in x for v in item]
labels = [["A"], ["B1", "B2"], ["C1", "C2", "C3"]]
labels_flatten = [v for item in labels for v in item]


def percentify(percent_num, total=100):
    return "{:.1f}%".format(percent_num/total*100)

f, ax = plt.subplots(2, 3, figsize=(14, 8))
ax = ax.ravel()

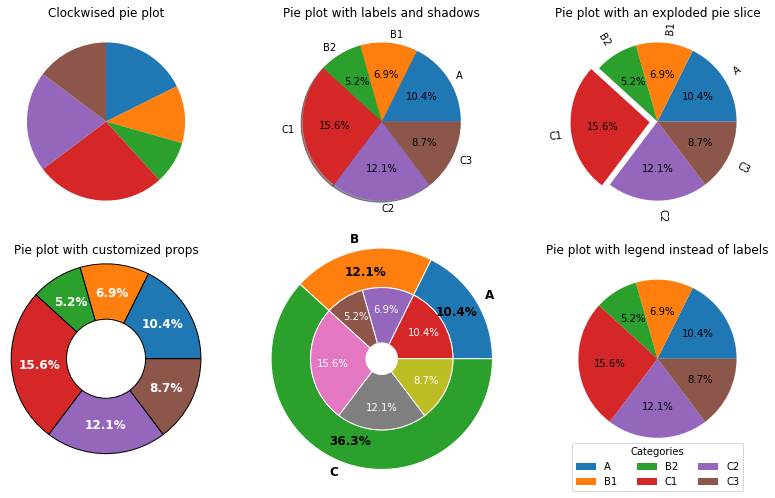
ax[0].pie(x_flatten, startangle=90, counterclock=False)
ax[0].set_title("Clockwised pie plot")

ax[1].pie(x_flatten, labels=labels_flatten, shadow=True,
          autopct=lambda k: percentify(k, sum(x_flatten)))
ax[1].set_title("Pie plot with labels and shadows")

explodes = np.zeros(len(x_flatten))
explodes[3] = 0.1  # 只炸开第4个扇形区
ax[2].pie(x_flatten, labels=labels_flatten,
          autopct=lambda k: percentify(k, sum(x_flatten)),
          explode=explodes, rotatelabels=True)
ax[2].set_title("Pie plot with an exploded pie slice")

ax[3].pie(x_flatten, radius=1.2, pctdistance=0.7,
          autopct=lambda k: percentify(k, sum(x_flatten)),
          textprops=dict(color='w', weight='bold', size=12),
          wedgeprops=dict(edgecolor='black', width=0.7))
ax[3].set_title("Pie plot with customized props")

x_outer = [sum(k) for k in x]
r, width_outer, inner_blank = 1.4, 0.5, 0.2
width_inner = r-width_outer-inner_blank
ax[4].pie(x_outer, radius=r, textprops=dict(size=12, weight='bold'),
          wedgeprops=dict(width=width_outer, edgecolor='w'),
          autopct=lambda k: percentify(k, sum(x_outer)),
          pctdistance=r-1.2*width_outer, labels=list("ABC"))
ax[4].pie(x_flatten, radius=r-width_outer,
          textprops=dict(color='w'),
          wedgeprops=dict(width=width_inner, ec='w'),
          autopct=lambda k: percentify(k, sum(x_flatten)),
          pctdistance=inner_blank+.7*width_inner)

patches, texts, autotexts = \
    ax[5].pie(x_flatten, autopct=lambda k: percentify(k, sum(x_flatten)))
ax[5].legend(patches, labels_flatten, title="Categories", ncol=3,
              loc="upper center", bbox_to_anchor=(0.5, 0.1))
ax[5].set_title("Pie plot with legend instead of labels")

plt.show()

箱型图：ax.boxplot

箱型图（也称盒须图）可以认为是五数概括（five number summary，即两个最值与三个四分位值；但最值的定义有所不同，下详）的一种可视化，主要由两部分组成：箱子与离群值（outliers）区。因为这几个概念的理解直接影响箱型图的读图，所以下面先简要谈谈这几个概念：

箱子：箱型图的主体当然是中间的箱子，其顶部一般对应上四分位值（或第三四分位，Q3，the 3rd quartile），即75分位值；底部一般是下四分位值Q1，即25分位值；这两个值之差（即箱子的高）称为四分位距（IQR，Interquartile range）。箱子中心的那根线是中位数（也即Q2）。所有的箱型图一般都遵循以上原则。
离群值区：不同箱型图的离群值区域规定可以不同。常见的方法是 Tukey 围栏（Tukey’s fences）定义的闭区间：

\begin{equation*} T(w) = [Q_1 - w\cdot IQR, Q_3 + w\cdot IQR] \end{equation*}

其中，\(w\) （须，whisker）是一个非负常数，而 \(IQR=Q_3-Q_1\) 即是上文提到的四分位距。下面是最朴素、可能也是最常见的离群值规则：
- 当 \(w=0\) 时，该围栏表示箱子的主体。
- 当 \(w=1.5\) 时，除了箱子主体，该围栏也将适度离群值（mild outliers）包括在内。
- 当 \(w=3\)，时，除了箱子主体与适度离群值，该围栏也将极限离群值（extreme outliers）包括在内。在箱型图中，有时把此时围栏的上下限称为“最值”（虽然我本人并不太赞同这种称呼）；这个最值与数据集的最值是不同的（因为还可能有在 \(T(3)\) 围栏外侧的点），注意区分。
- 对于更外侧的情形，这部分数据点有时也被标记为 far out。

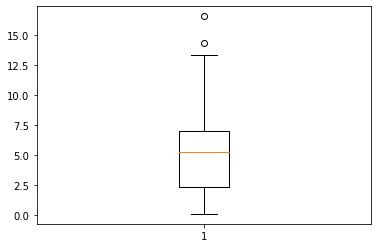
一个简洁的箱型图例子。

箱体中的橙色线是中位数。
箱体两侧的须的末端，标明了 \(T(w)\) 围栏的两个端点。
在 \(T(w)\) 围栏外侧的数据被称为异常值点（fliers），会单独以圆圈点的形式绘制出来。

Matplotlib 中的默认围栏取 \(w=1.5\)，即它认为极限离群值属于异常值。

[10]:

np.random.seed(0)
x = np.concatenate((np.random.rand(90)*10, np.random.rand(10)*20))

f, ax = plt.subplots()
ax.boxplot(x)
plt.show()

箱型图的常用参数

箱型图的绘制命令：

ax.boxplot(x, whis=1.5, vert=True, ...)

x：一维或多维的数据。
whis：须（whisker）值，影响绘制时围栏的上下端点。默认是 1.5。
vert：默认 True，即以竖直方式绘图。
widths：箱型图在绘制时的箱体宽度。
labels：每个箱型图的标签。
notch：切口箱型图。切口在中位数处，切口宽度是中位数的 95% 置信区间。
- 当 notch=True 时，可配合使用 bootstrap=True 来使用 bootstrap 来估计该置信区间。
绘图参数：
- 箱子主体：显隐 showbox，外观 boxprops。注意：箱子的前景色只能在 patch_artists=True 时使用。
- 异常值点：显隐 showfliers，外观 filerprops
- 须：须外观 whiskerprops
  - 须的末端线的显隐 showcaps，须的末端线外观 capprops，
- 中位数线：显隐 showmedians，外观 medianprops
- 均值点/线（默认关闭）：显隐 showmeans，按线显示 meanline，外观 meanprops

下面的例子涵盖了上述所有参数：

[11]:

mu_shared, r = 5, [1, 5, 3]
np.random.seed(0)
x = np.random.rand(100, 3) * r + mu_shared
np.random.seed(123)
x = np.concatenate((x, np.random.rand(10, 3) * 3))

f, ax = plt.subplots(2, 3, sharey='col', figsize=(14, 8))
f.subplots_adjust(hspace=0.3)
ax = ax.ravel()

colors = {"line": 'tab:red', "face": 'lightblue'}
g = ax[0].boxplot(x, patch_artist=True, labels=list("ABC"))
for line in ['boxes', 'whiskers', 'means', 'medians', 'caps']:
    plt.setp(g[line], color=colors["line"])
## 论外的箱子前景色与异常值点的颜色。
plt.setp(g['fliers'], mec=colors["line"])  # mec=markeredgecolor，参考第一章
plt.setp(g['boxes'], facecolor=colors["face"])  # 前景色需要 patch_artist=True
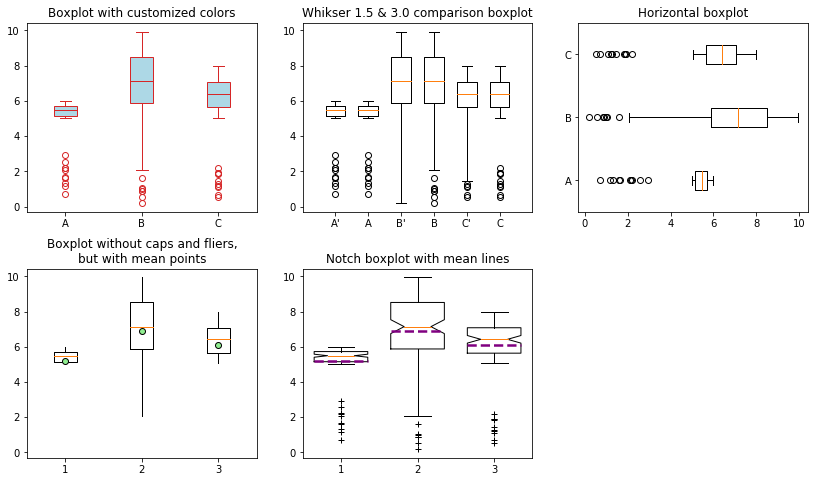
ax[0].set_title("Boxplot with customized colors")

ax[1].boxplot(x, whis=3, labels="A' B' C'".split())
ax[1].boxplot(x, positions=np.arange(3)+1.5, labels=list("ABC"))
ax[1].set_title("Whikser 1.5 & 3.0 comparison boxplot")

ax[2].boxplot(x, vert=False, labels=list("ABC"))
ax[2].set_title("Horizontal boxplot")

ax[3].boxplot(x, showcaps=False, showfliers=False, showmeans=True,
              meanprops=dict(marker='o', mec='black', mfc='lightgreen', ms=6))
ax[3].set_title("Boxplot without caps and fliers,\nbut with mean points")

ax[4].boxplot(x, widths=0.7, showmeans=True, meanline=True, notch=True,
              meanprops=dict(ls='--', lw=2.5, color='purple'),
              flierprops=dict(marker='+'))
ax[4].set_title("Notch boxplot with mean lines")

ax[5].axis('off')

plt.show()

箱型图的细节概念*

本节是针对不太了解箱型图的读者的补充内容。对箱型图概念很熟悉的读者可以跳过。

我们来看一个模拟的例子：用符合正态分布 \(N(0,1)\) 的一维数据，模拟一下 Tukey 围栏：

[12]:

from scipy.stats import norm

mu, sigma, n = 0, 1, 5000
np.random.seed(1234)
x = np.random.normal(mu, sigma, n)

q1, q3 = np.percentile(x, 25), np.percentile(x, 75)
w, iqr = 1.5, q3 - q1
bpmin, bpmax = q1 - w*iqr, q3 + w*iqr

f, ax = plt.subplots(2, 1, sharex=True, gridspec_kw={'height_ratios':[3, 7]})
ax = ax.ravel()

# 绘制箱型图
ax[0].set_title("Boxplot & density plot of Normally choosen data")
ax[0].boxplot(x, vert=False, labels="X")
## 标出关键值的位置
maxmincolor, boxcolor = 'tab:blue', 'tab:orange'
[ax[0].axvline(lines, color=maxmincolor) for lines in (bpmin, bpmax)]
[ax[0].axvline(lines, color=boxcolor) for lines in (q1, q3)]

# 绘制 0.01%~99.99% 累计概率范围内的真实正态密度曲线
plt_x =  np.linspace(norm.ppf(.0001, mu, sigma),
                     norm.ppf(.9999, mu, sigma), n)
plt_y = norm.pdf(plt_x)
ax[1].plot(plt_x, plt_y, 'r')
## 显示 Tukey 围栏的数据
ax[1].text(-4, 0.3, f'box | min, max\n= {q1:.2f}, {q3:.2f}', color=boxcolor)
ax[1].text(-4, 0.2, f'{w} whisker | min, max\n= {bpmin:.2f}, {bpmax:.2f}', color=maxmincolor)

plt.show()

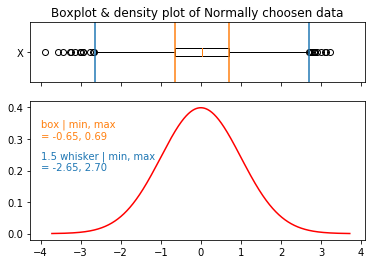
上例中：

模拟得到的箱子上下限（Q1, Q3）是：-0.65, 0.69
模拟得到的 \(w=1.5\) 的 Tukey 围栏上下限是： -2.65, 2.70.

而理论值（只针对数据服从标准正态分布的情形）是：

[13]:

q1_theory = norm.ppf(.25, mu, sigma)
q3_theory = norm.ppf(.75, mu, sigma)
iqr_theory = q3_theory - q1_theory
bpmin_theory = q1_theory - w * iqr_theory
bpmax_theory = q3_theory + w * iqr_theory
tukey_prob = norm.cdf(bpmax_theory) - norm.cdf(bpmin_theory)

print(f"Q1 = {q1_theory:.4f}, Q3 = {q3_theory:.4f}, 覆盖了 0.50 概率范围；\n" +
      f"T({w}) = [{bpmin_theory:.4f}, {bpmax_theory:.4f}]，覆盖了 {tukey_prob:.4f} 概率范围。")

Q1 = -0.6745, Q3 = 0.6745, 覆盖了 0.50 概率范围；
T(1.5) = [-2.6980, 2.6980]，覆盖了 0.9930 概率范围。